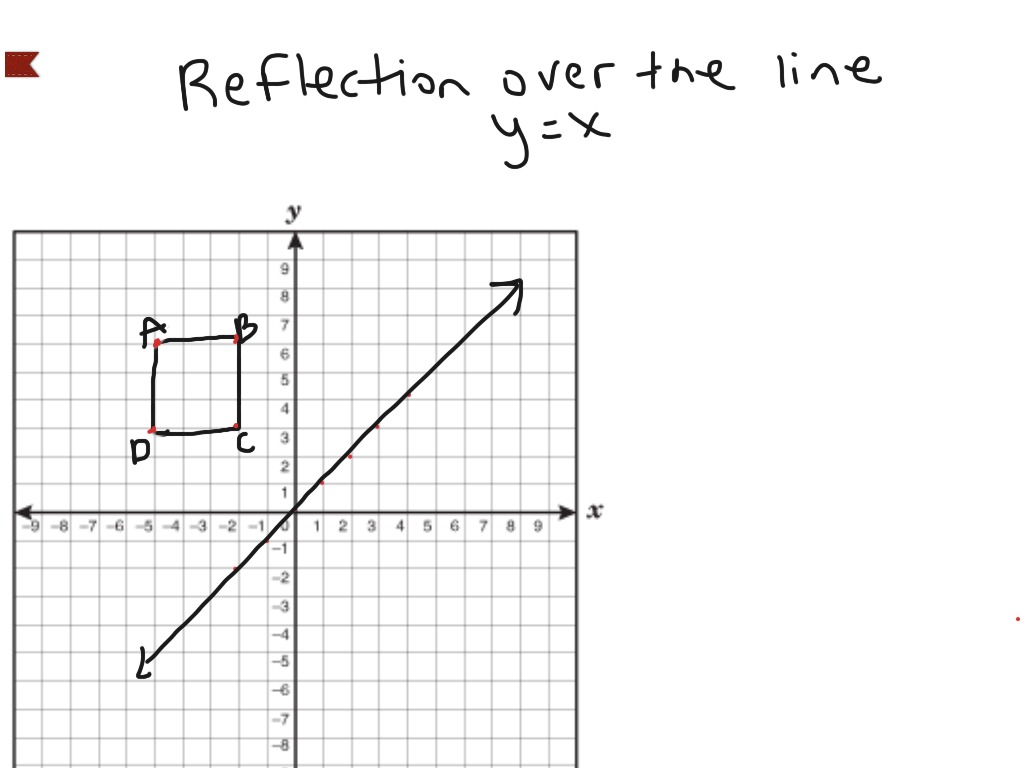
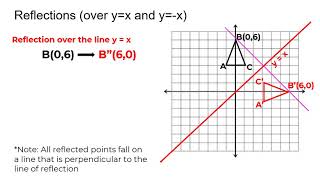
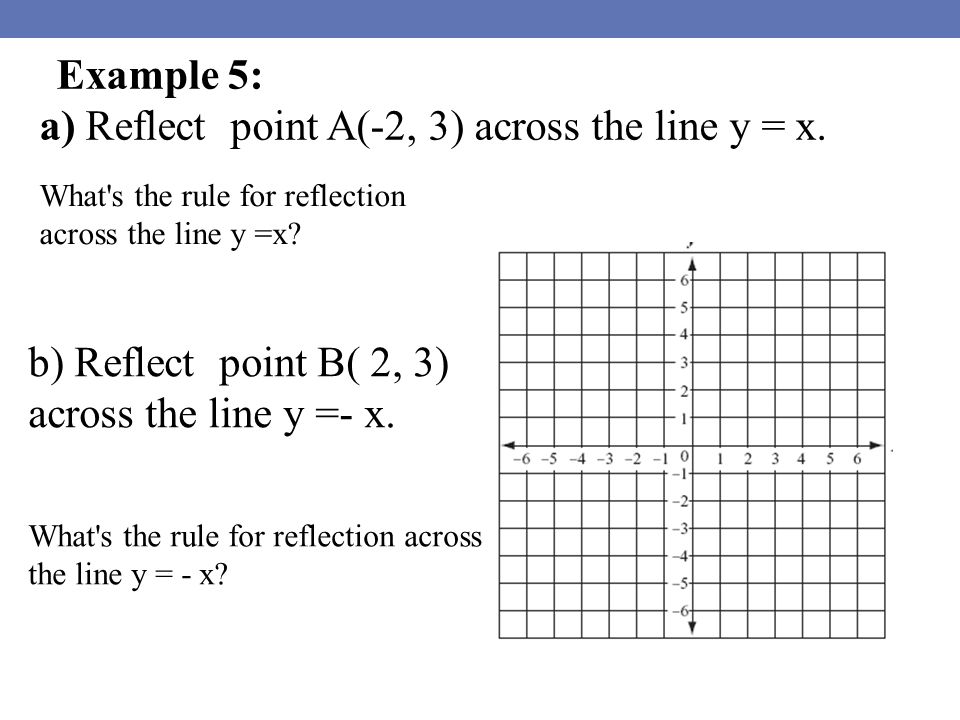
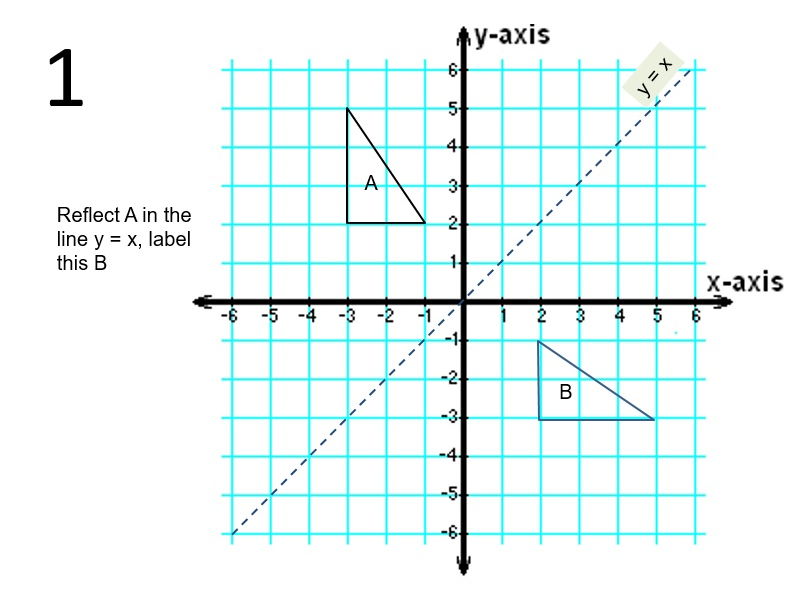
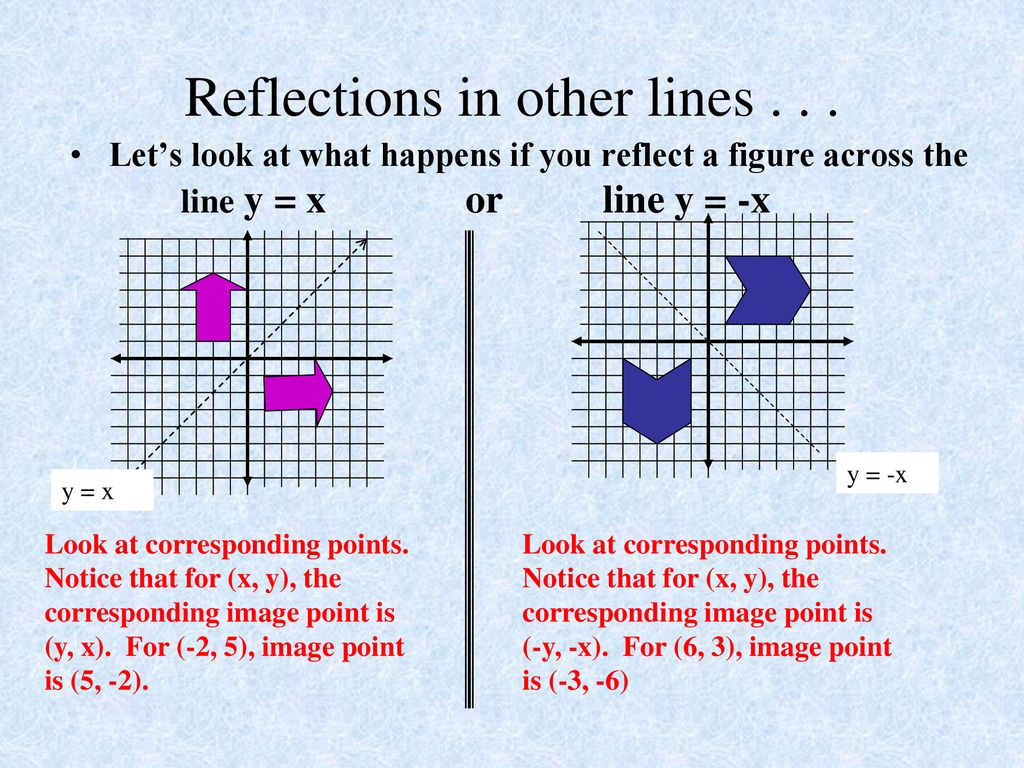
Reflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflectionReflection over y=x when reflecting a point across the line y=x, both changes (y,x) Reflection over y=x When you reflect a point across the line y = x, both change places and are negated (y,x) Reflection over the origin (y,x) Rotation of 90 (y,x)13 Another way To reflect along a line that forms an angle θ with the horizontal axis is equivalent to rotate an angle − θ (to make the line horizontal) invert the y coordinate rotate θ back Further, y = mx implies tanθ = m, and 1 m2 = 1 cos2θ Then,
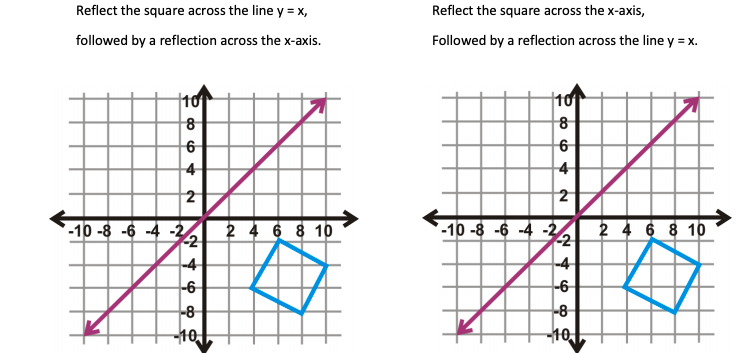
Reflect The Square Across The Line Y X Followed By Chegg Com
Reflection in line y=x matrix
Reflection in line y=x matrix- line segments I end this segment i n over here and T oh this is T oh here are reflected over the line y is equal to negative X minus 2 so this is the line that they're reflected about this dashed purple line and it is indeed y equals negative X minus 2 this right over here is in slopeintercept form the slope should be negative 1 and we see that the slope of this purple line isGraph the line Ask students to start with point A and reflect it over the line My students told me to go left 2 squares to get to y = xx and then 2 more squares past that to create the new line While this is the method we learned for reflecting points over a line, we always had a horizontal or vertical line, not a diagonal line




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
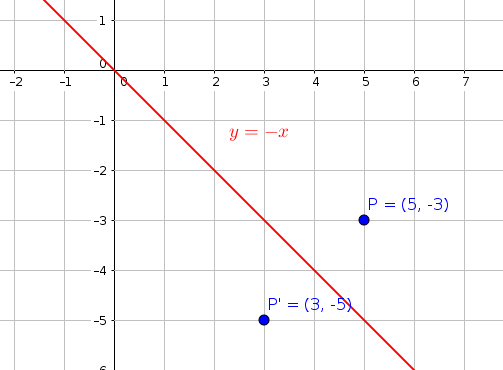
It is easier to understand reflection with an example The diagram below shows a reflection of a shape The shape before the reflection (called the object) is in light blue The shape after the reflection (called the image) is in dark blue In this example, the shape has reflected in a line of reflection (shown as a red dashed line) on the yaxisReflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxisA shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinate
Let P (x, y) be any point in the 2D coordinates plane The reflection of this point P (x, y) in x axis is clearly the point P' (x, y) Similarly the reflection of the P' in the line y =Linear Algebra, Reflection through a LinePoint Q is the reflection of point P through the line AB In a plane (or, respectively, 3dimensional) geometry, to find the reflection of a point drop a perpendicular from the point to the line (plane) used for reflection, and extend it the same distance on the other side
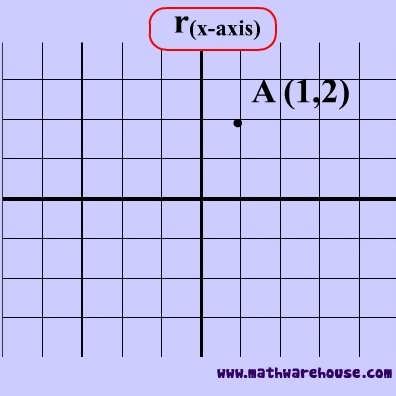
O a reflection through the origin O a reflection over the line y = x O a dilation with a scale factor of 1 centered at (2,3) a dilation with a scale factor of centered at the origin Categories English Leave a Reply Cancel reply Your email address will not be published Required fields are marked *Click here👆to get an answer to your question ️ The point A (4,1) undergoes following transformations successively (i) reflection about line y = x (ii) translation through a distance of 3 units in the positive direction of x axis(iii) rotation through an angle 105 ^ ∘ in anti clockwise direction about origin O Then the final position of point A is A reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image In this case, the x axis would be called the axis of reflection Math Definition Reflection Over the Y Axis
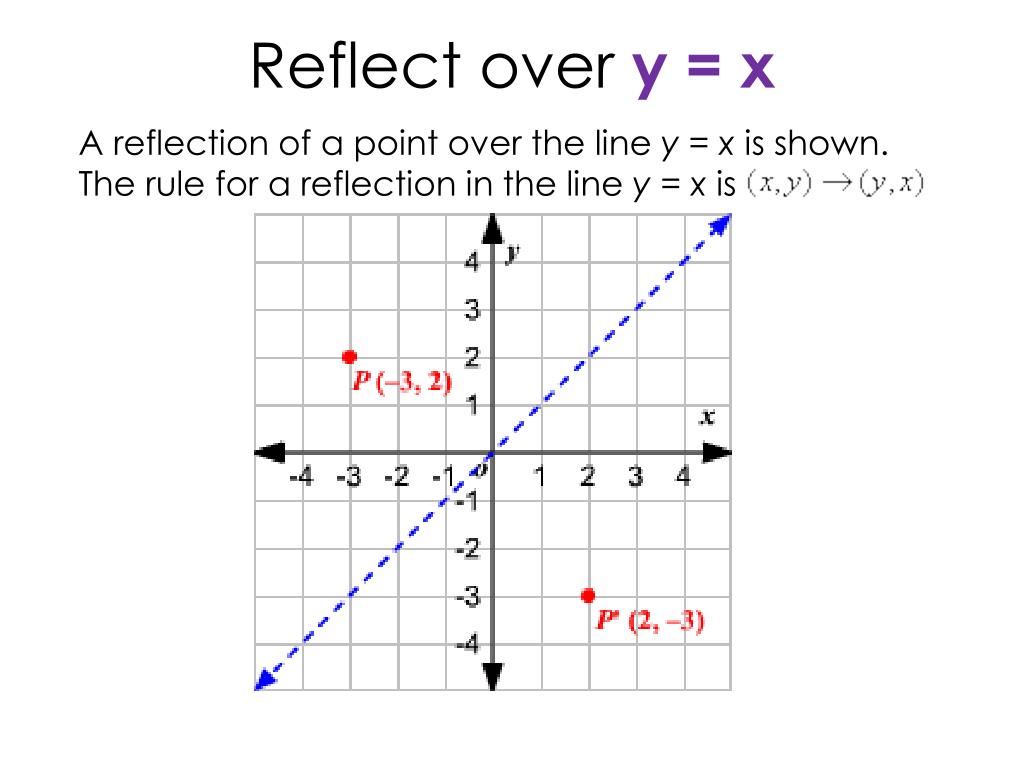



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id
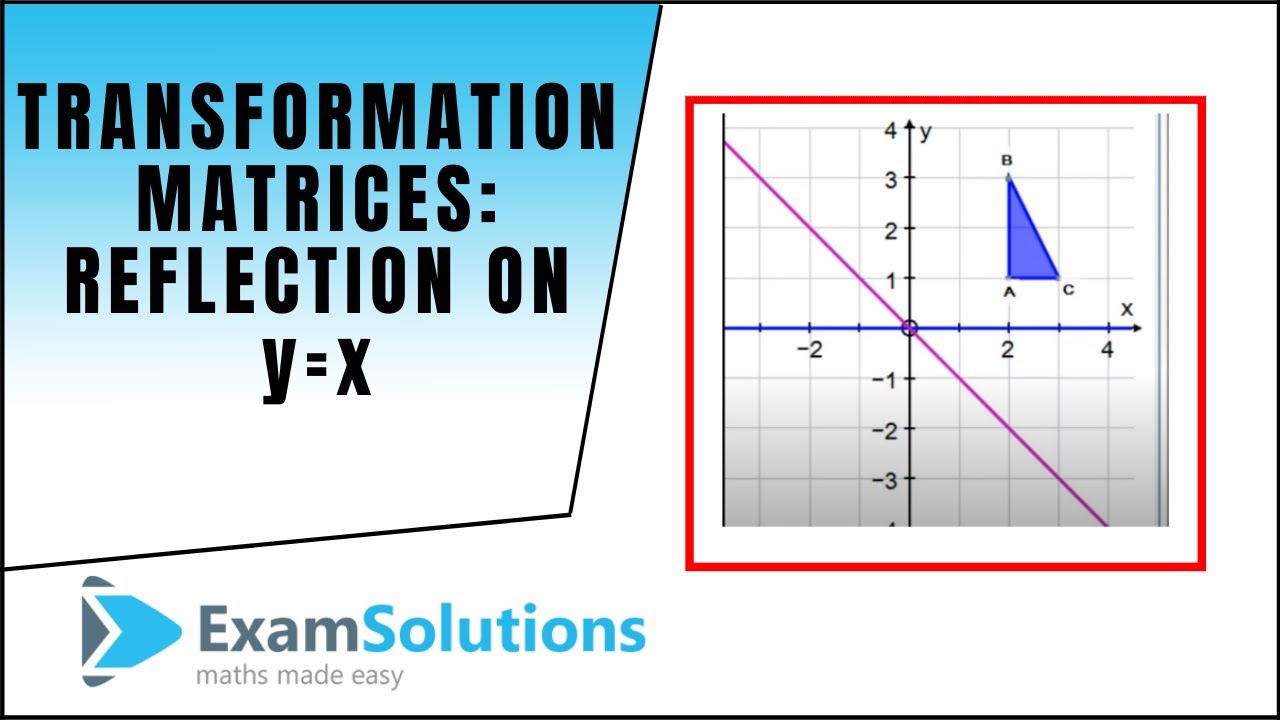



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube
or y = x (2, 2) (4, 4) (5, 5) Just plotting a few of these coordinates will make sure that you always reflect in the correct mirror line The only other issue is to make sure that your reflection is at 90 degrees to the line, and it's the same distance both sides Other than that, you're good to go Here's some videos to helpUsually you should just use these two rules T (x)T (y) = T (xy) cT (x) = T (cx) Where T is your transformation (in this case, the scaling matrix), x and y are two abstract column vectors, and cREFLECTIONS Reflections are a flip The flip is performed over the "line of reflection" Lines of symmetry are examples of lines of reflection Reflections are isometric, but do not preserve orientation Coordinate plane rules Over the xaxis (x, y) (x, –y) Over the yaxis (x, y) (–x, y)




Reflection Matrix About Line Y X Tan 8 C Geogebra




Reflection Mathbitsnotebook A1 Ccss Math
One must remember that, when the reflection axis is a line in the XY plane, say Xaxis, the rotation path about this Xaxis is in a plane which is perpendicular to the XY plane So Image gets reflected with respect to any axis say Xaxis or Yaxis Generally the image is original plane is represented with the points say 1,2,3, where as the If m = 0, then the line x = 0 is perpendicular to the line y = 0 at the origin In either case the vector − m 1 is on the perpendicular line Thus, by the reflection across the line y = m x, this vector is mapped to m − 1 That is, we have Homework Statement Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a Solution




S1 Work For Problem Ii About Reflection Respect To The Y X Line But Download Scientific Diagram



Translation Geometry
Reflection Transformations in 2Space Let such that and suppose that we want to reflect across the axis as illustrated Thus the coordinate of our vector will be the opposite to that of our image The following equations summarize our image Thus our standard matrix is , and in form we get that Of course there are other types of reflectionMatrices for Reflections 257 Lesson 46 This general property is called the Matrix Basis Theorem Matrix Basis Theorem Suppose A is a transformation represented by a 2 × 2 matrix If A (1, 0) → (x 1, y 1) and A (0, 1) → (x 2, y 2), then A has the matrix x 1 x 2 y 1 y 2 Proof Let the 2 × 2 transformation matrix for A be abSee the answer Show transcribed image text Expert Answer 100% (1 rating) Previous question Next question



Reflection



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
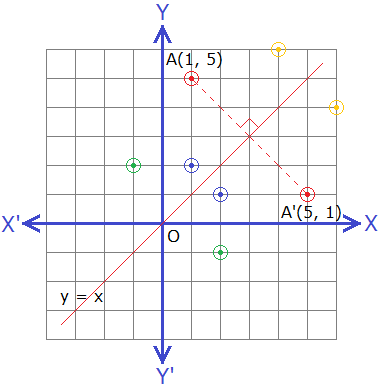
File previews pdf, 975 KB Worksheet for students to use to reflect shapes in the x and y axes Also reflecting in the line y=x (diagonal line bottom left to top right) Tes classic free licence Report this resource to let us know if it violates our terms and conditions Our customer service team will review your report and will be in touch Reflection in a Line 4 Reflecting over the line y = x or y = x (the lines y = x or y = x as the lines of reflection) When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change placesThe resulting orientation of the two figures are opposite



1




Learn About Reflection Over The Line Y X Caddell Prep Online
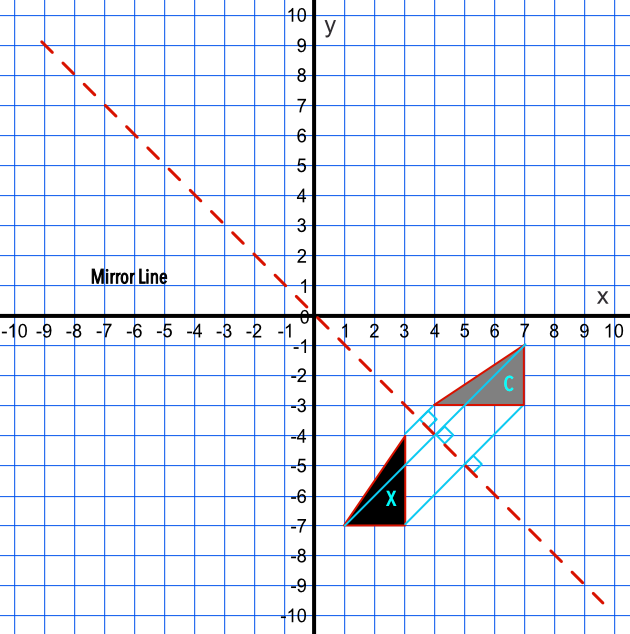
Because (k,k) has to be a point on the line y = x, a point on the mirror line Any point on the mirror line is equidistant from original point and it's reflection And obviously these two points (1, 7) and (7, 1) are reflection of the line y = x So here we can get a visual of it, and we can actually see these various isosceles triangleTo describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1\) is a vertical line which passes through 1 onSince point A is located three units from the line of reflection, we would find the point three units from the line of reflection from the other side The yvalue will not be changing, so the coordinate point for point A' would be (0, 1) Repeat for points B and C In the end, we found out that after a reflection over the line x=3, the



Reflection



1
Find an equation of the image of the line under multiplication by 17 In parts (a) through (e), find an equation of the image of the line under (a) a shear of factor 3 in the xdirection (b) a compression of factor in the ydirection (c) a reflection about (d) a reflection about the yaxis (e) a rotation of 60° about the origin AnswerReflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)KCET 12 The reflection of the point (1,1) along the line y = x is (A) (0,0) (B) (1,1) (1,1) (D) (1,1) Check Answer and Solution for abo




Reflection In The Line Y X Geogebra



10 Math Problems Transformation Reflection
Reflection Across Y=X When reflecting over the line y=x, we switch our x and y, and make both negative Reflection Over Y = X In order to define or describe a reflection, you need the equation of the line of reflection The four most common reflections are defined below 1 Start by rearranging the equation of the mirror line into 2 3x − y = − 8 3 The normal form of the equation of a line is n ⋅ x = const, where n is some vector normal (perpendicular) to the line Comparing this to the mirror line equation, I see that a normal to it is (2 3, − 1) Since any normal will do, I'll multiply this by − 3The line that represents y=x has a slope of 1/1 If i am considering a point, ill refer to it as A at (4,3) and reflect it over line y=x i will be at (4,3) which i will refer to as point B I can prove this relationship using simple geometry I wi




Reflection Mathbitsnotebook A1 Ccss Math




How To Reflect A Graph Through The X Axis Y Axis Or Origin
Question Parti) Reflect The Vector Through The Line Y=0 Resultant Vector Part Ii) Reflect The Vector 1 Through The Line Y=1 Resultant Vector This problem has been solved!If (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed;The equation of the line of the mirror line To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1




Reflection Mathbitsnotebook A1 Ccss Math



Reflection Over The Line Y X Math Showme
Reflections A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflectionTranscribed Image Textfrom this Question Find the standard matrix of the composite transformation from R^2 to R^2 Reflection in the line y = x, followed by counterclockwise rotation through 60 degree, followed by reflection in the line y=xAs you can see in the above graphic, logarithms are truly inverses of exponential functions since it is a reflection over the line y=x Logarithmic functions behave in similar ways as our more familiar functions do we can stretch, compress, reflect, and translate them For instance, y=2*log x



Math Alive Geometry 1



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N
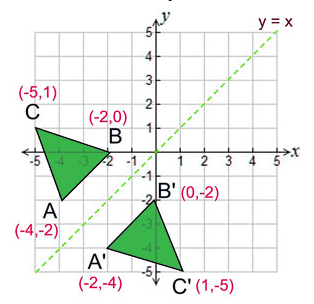
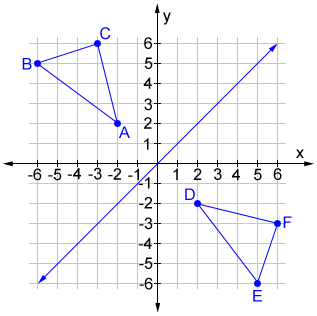
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xReflections and Rotations We can also reflect the graph of a function over the x axis (y = 0), the y axis (x = 0), or the line y = x Making the output negative reflects the graph over the x axis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x)A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6) Triangle DEF has vertices D (2, 2), E (5, 6), and F (6, 3)



Reflections




Reflection Rules How To W 25 Step By Step Examples
Reflection can be found in two steps First translate (shift) everything down by b units, so the point becomes V=(x,yb) and the line becomes y=mxThen a vector inside the line is L=(1,m)Now calculate the reflection by the line through the origin,Reflection over the line y = x A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = x (A, B) → (B, A) From the diagram we see the object point ( − 2, −5) is mapped to (x',y') by a reflection in the line X = 2 we note (1) the ycoordinate is unaffected (2) for reflections the distance from the line of reflection to the object is equal to the distance to the image point ∴ a = 2 2 = 4units so the image point is 4 units from the line of




Reflecting Shapes Article Reflections Khan Academy



Reflection Over The Y X Line Youtube
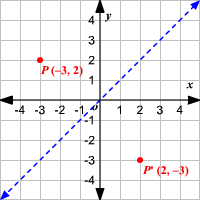
A point reflection is just a type of reflection In standard reflections, we reflect over a line, like the yaxis or the xaxisFor a point reflection, we actually reflect over a specific point, usually that point is the origin $ \text{Formula} \\ r_{(origin)} \\ (a,b) \rightarrow ( \red a , \red b) $




Transformations Of Graphs




Reflection Transformation Matrix




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com



1 Geometry Ms Singarajah 7



Reflection An Isometry Or Rigid Motion In Which A Figure Is Flipped Giving Its Image An Opposite Orientation Ppt Download




How To Find A Reflection Image



Reflection Definition Reflection In The Coordinate Plane



Diagonal Reflections In The Line Y X Teaching Resources
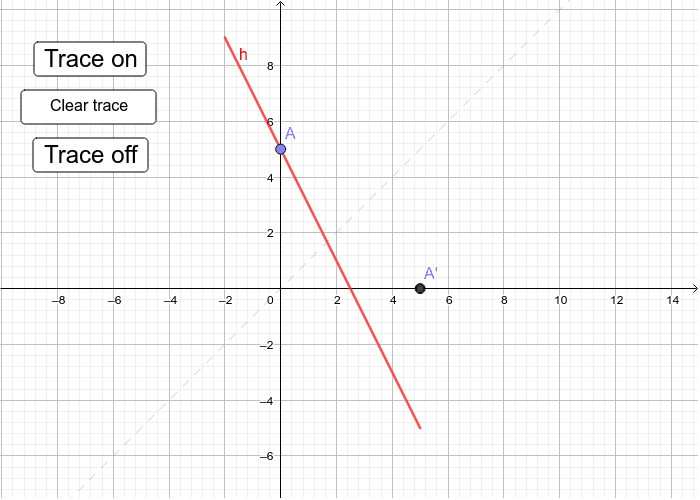



Reflecting In The Line Y X 2 Geogebra




Reflection Transformation Matrix



Geometric Reflections Q35 50 Intro To Geometry




Image Point Coordinates After Reflection Across Any Line Youtube




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



1




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflect The Square Across The Line Y X Followed By Chegg Com




Coordinate Geometry Reflections On A Coordinate Plane Magoosh Math




Reflection Over The Y X Line Youtube
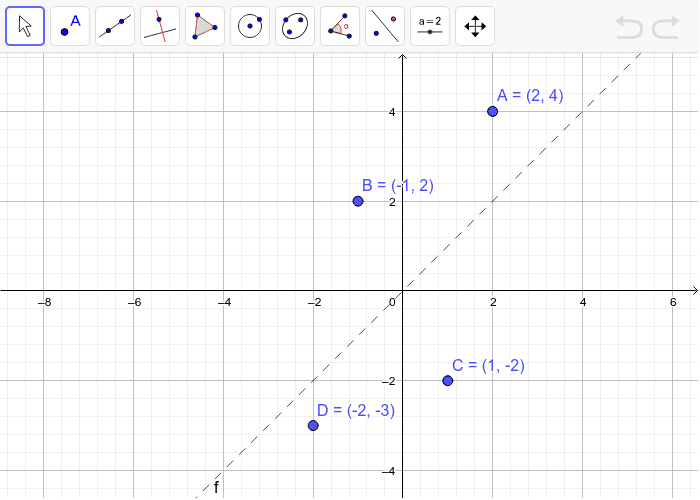



Reflecting In The Line Y X 2 Geogebra
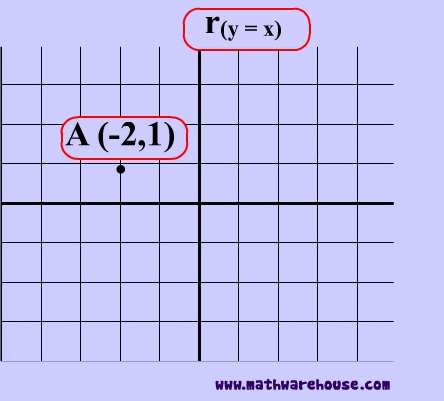



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
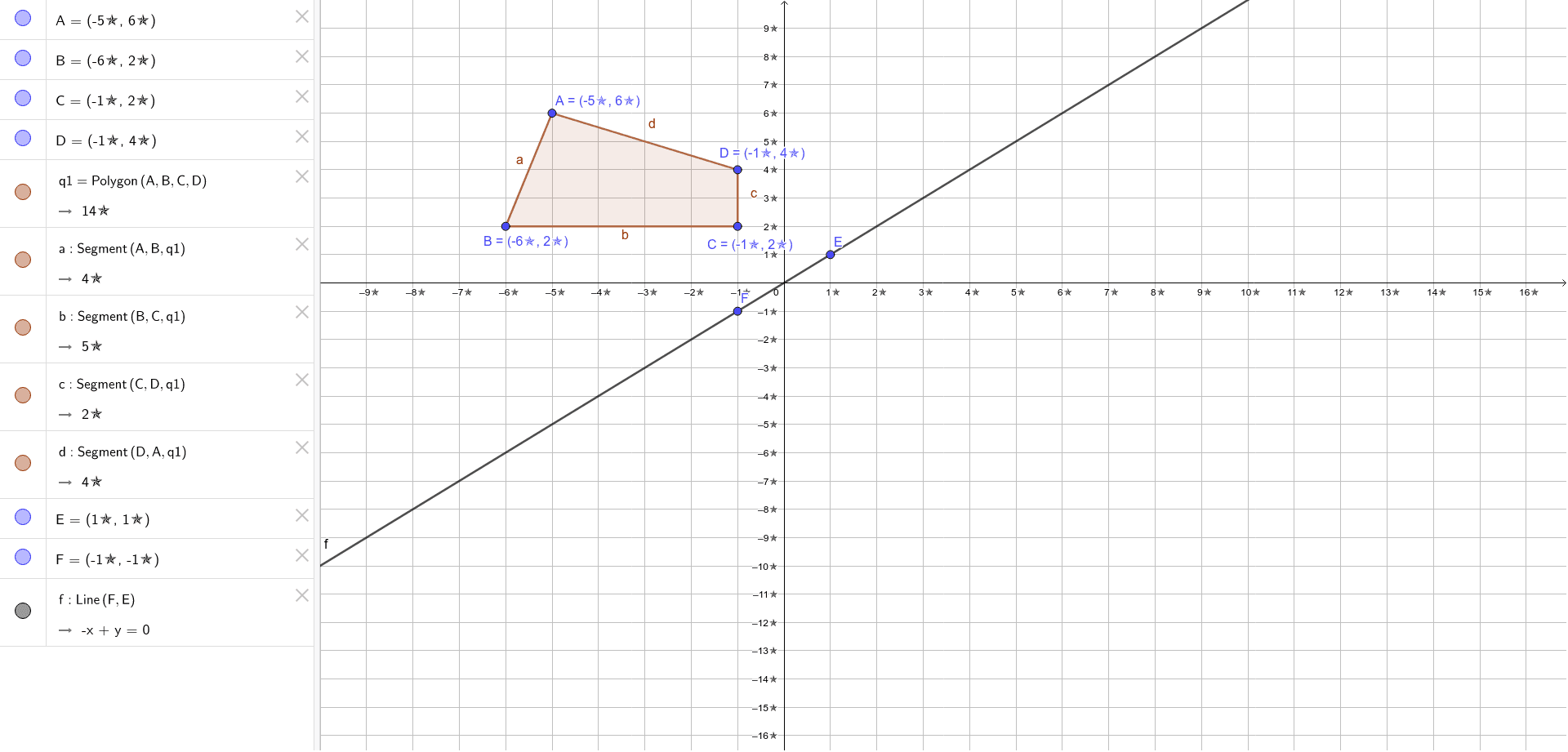



Reflection Across The Line Y X Geogebra




Describing A Reflection Key Stage 2




Reflecting Shapes Article Reflections Khan Academy



Transformations Dilations Translations Reflections Rotations Ppt Download



Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflection Rules How To W 25 Step By Step Examples




Reflection Over The Line Y X Geogebra




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




Reflection Over The Line Y X Youtube




Reflection Mathbitsnotebook A1 Ccss Math




Reflection In The Line Y X Transformation Matrix Youtube




The Equation Of A Line Reflected About Another Line Mathematics Stack Exchange




In The Figure Shown Triangle Rst Undergoes Reflections Across Two Line R S T Is The Final Brainly Com




Reflection Transformation Matrix




Reflection Mathbitsnotebook A1 Ccss Math




Reflections Through The Axes And The Lines Y X And Y X Geogebra




Reflection Over Y 2 With Rule Educreations




How To Reflect A Graph Through The X Axis Y Axis Or Origin




Reflecting Functions Examples Video Khan Academy




Reflection Over Y X Math Geometry Showme



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Picture Of Reflection In The Line Y X Reflection Math Math Reflection



What Is The Reflection Image Of 5 3 In The Line Y X Socratic
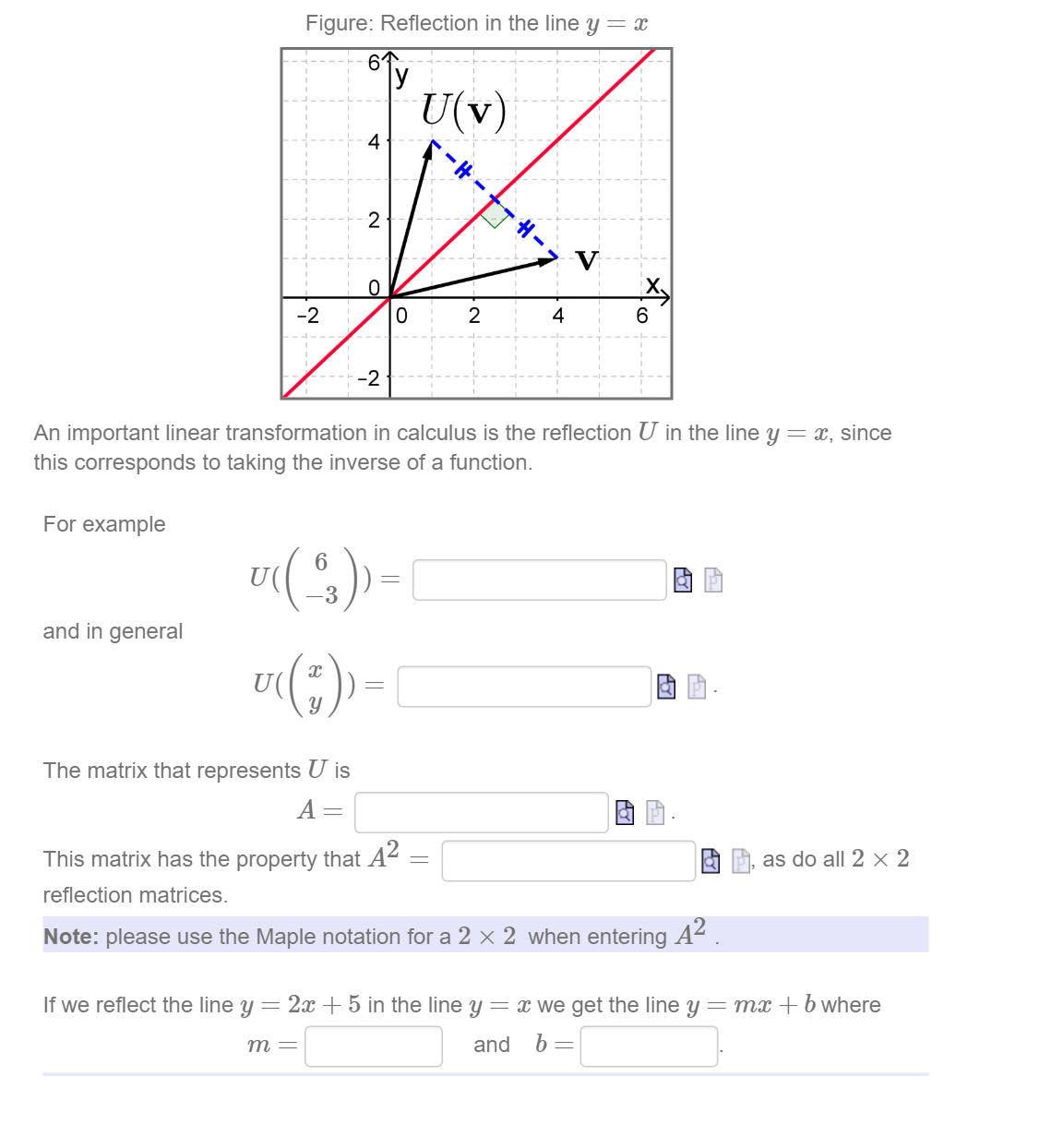



An Important Linear Transformation In Calculus Is The Chegg Com



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora




Reflection Transformation Matrix
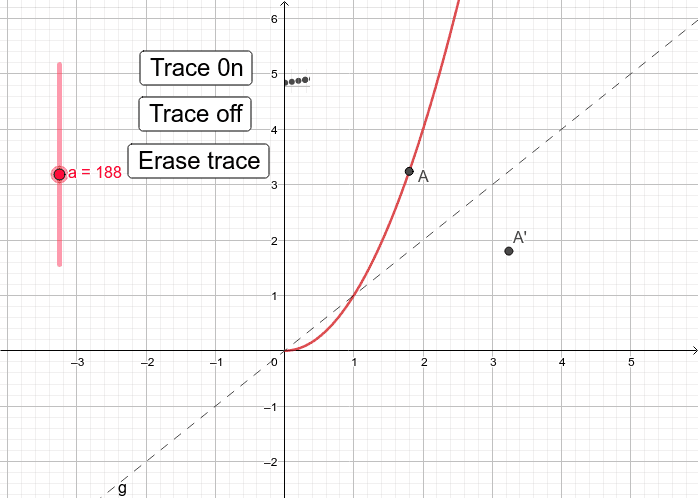



Reflecting In The Line Y X 2 Geogebra



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com




Reflection Over The Line Y X Math Showme




Reflection Rules How To W 25 Step By Step Examples



What Does It Mean To Reflect Over The Y X Line Quora




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
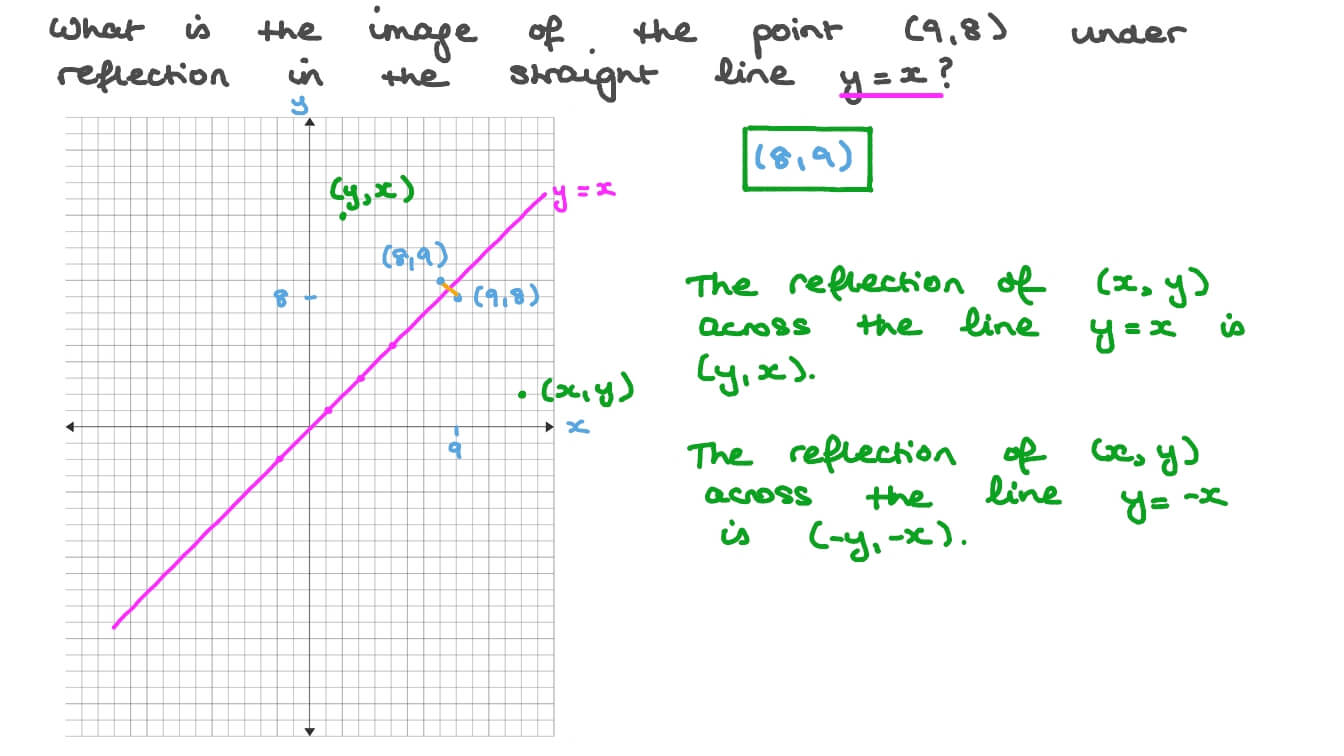



Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q




Common Reflections Key Stage 3
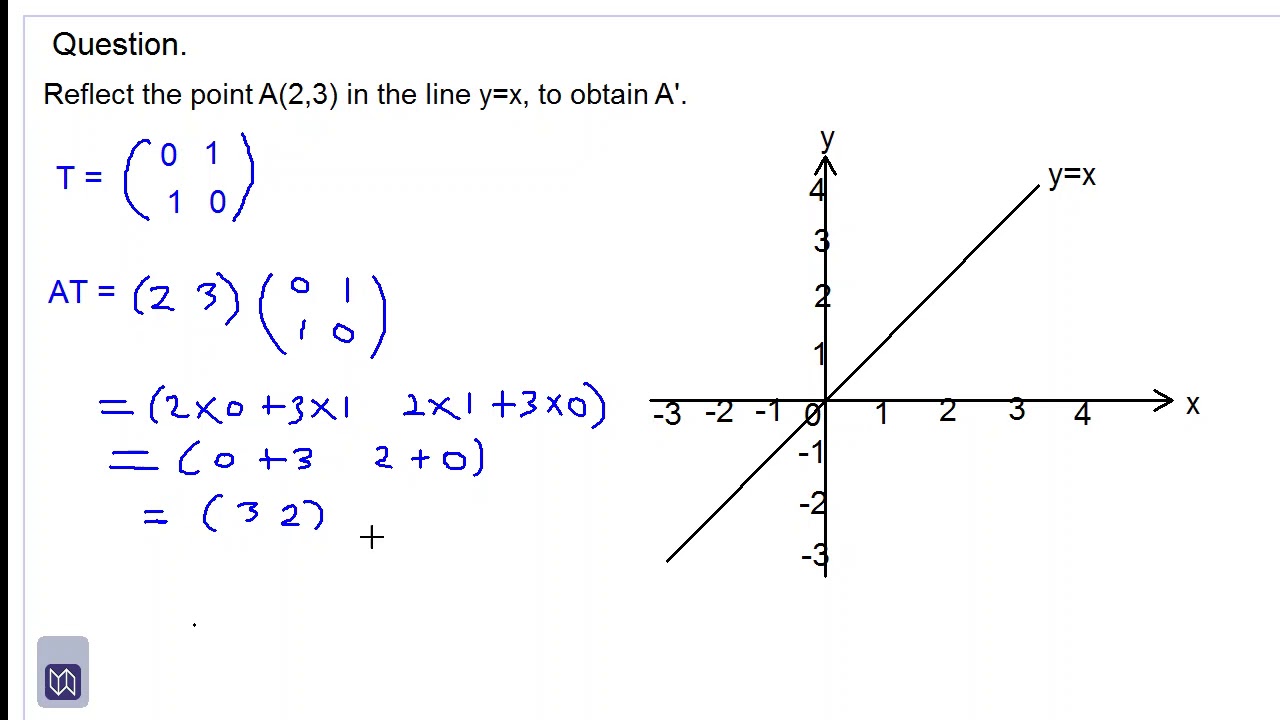



Transformation Matrix For Reflection In Y X Youtube




Reflection Over The X And Y Axis The Complete Guide Mashup Math




Transformation Reflection Over The Line Y X Youtube




Reflecting Shapes Article Reflections Khan Academy




Transformations Boundless Algebra
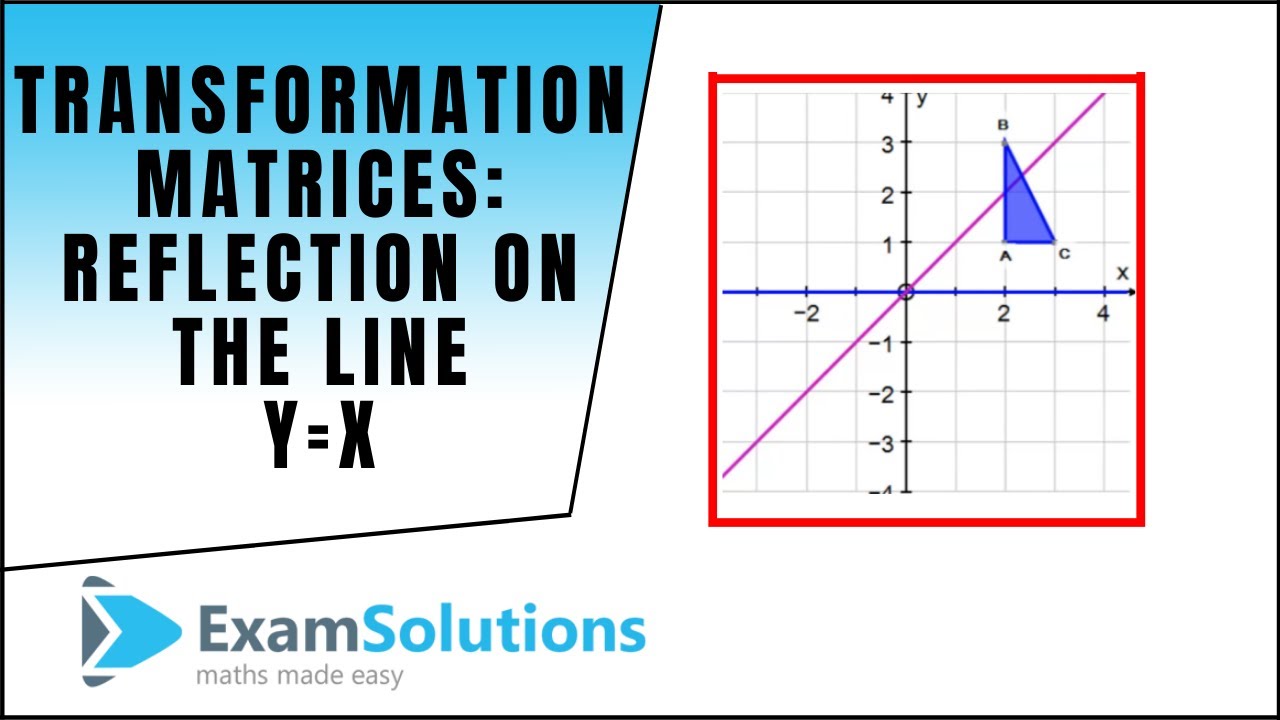



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube




Translation With Geogebra Figure 2 Reflection Through Line Y X With Download Scientific Diagram




Reflections Ck 12 Foundation




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
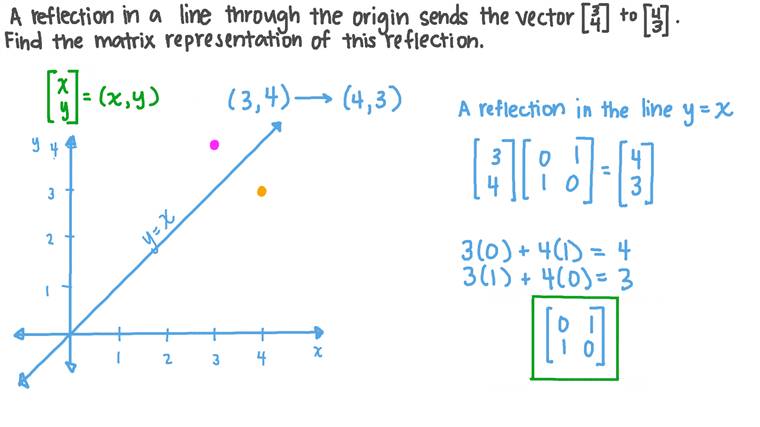



Lesson Linear Transformations In Planes Reflection Nagwa



Math Alive Geometry 1




Linear Transformations With Matrices Lesson 10 Reflection In The Line Y X Youtube




How To Find A Reflection Image



What Is The Reflection Of The Point 3 1 In The Line Y 2 Quora




Why Do Points Get Exchanged When Reflected Across Line Y X Quora
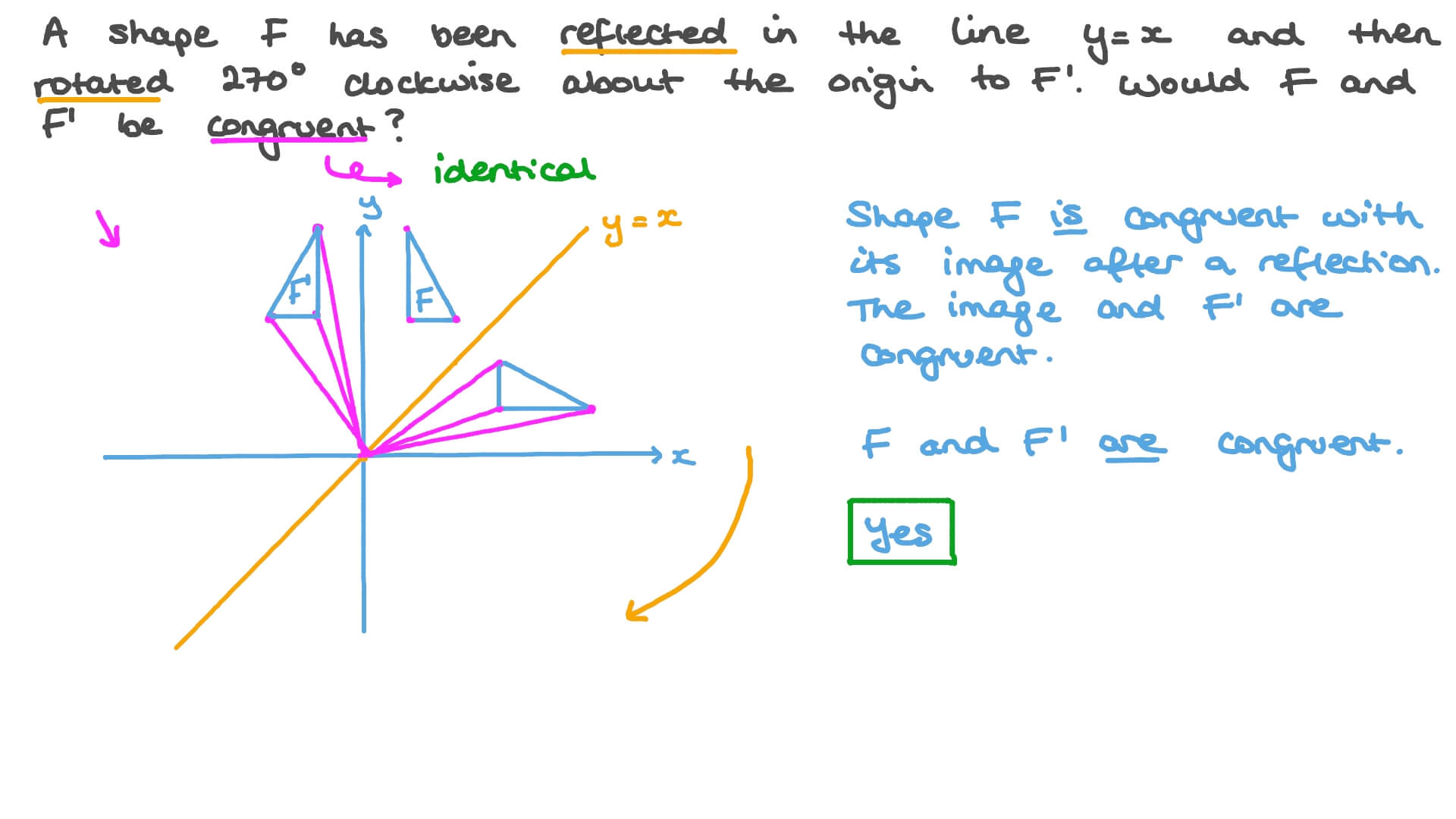



Question Video Understanding The Effects Of Reflection And Rotation On A Shape Nagwa




Solution What S The Result When We Reflect Y Sin X Twice Trigonometry Triangles To Functions Underground Mathematics




Reflection Definition Reflection In The Coordinate Plane



Reflecting Points Video Reflections Khan Academy



Reflection



0 件のコメント:
コメントを投稿